Adaptive Security in SNARGs via iO and Lossy Functions
|

|

|

| ||||||
|
We construct an adaptively sound SNARGs in the plain model with CRS relying on the
assumptions of (subexponential) indistinguishability obfuscation (iO), subexponential
one-way functions and a notion of lossy functions we call length parameterized lossy
functions. Length parameterized lossy functions take in separate security and input
length parameters and have the property that the function image size in lossy mode
depends only on the security parameter. We then show a novel way of constructing such
functions from the Learning with Errors (LWE) assumption.
Our work provides an alternative path towards achieving adaptively secure SNARGs from the recent work of Waters and Wu. Their work required the use of (essentially) perfectly re-randomizable one way functions (in addition to obfuscation). Such functions are only currently known to be realizable from assumptions such as discrete log or factoring that are known to not hold in a quantum setting.
@inproceedings{C:WatZha24,
author = {Brent Waters and Mark Zhandry}, booktitle = {CRYPTO~2024, Part~X}, editor = {Leonid Reyzin and Douglas Stebila}, month = aug, pages = {72--104}, publisher = {Springer, Cham}, series = {{LNCS}}, title = {Adaptive Security in {SNARGs} via {iO} and Lossy Functions}, volume = {14929}, year = {2024} } | |||||||||
Computational Wiretap Coding from Indistinguishability Obfuscation
|

| ||||||||
|
A wiretap coding scheme for a pair of noisy channels (B,E) enables Alice to reliably
communicate a message to Bob by sending its encoding over B, while hiding the message
from an adversary Eve who obtains the same encoding over E.
A necessary condition for the feasibility of writeup coding is that B is not a degradation of $\chE$, namely Eve cannot simulate Bob`s view. While insufficient in the information-theoretic setting, a recent work of Ishai, Korb, Lou, and Sahai (Crypto 2022) showed that the non-degradation condition is sufficient in the computational setting, assuming idealized flavors of obfuscation. The question of basing a similar feasibility result on standard cryptographic assumptions was left open, even in simple special cases. In this work, we settle the question for all discrete memoryless channels where the (common) input alphabet of B and E is binary, and with arbitrary finite output alphabet, under the standard assumptions that indistinguishability obfuscation and injective PRGs exist. In particular, this establishes the feasibility of computational wiretap coding when B is a binary symmetric channel with crossover probability p and E is a binary erasure channel with erasure probability e, where e>2p. On the information-theoretic side, our result builds on a new polytope characterization of channel degradation for pairs of binary-input channels, which may be of independent interest.
@inproceedings{C:IJLSZ23,
author = {Yuval Ishai and Aayush Jain and Paul Lou and Amit Sahai and Mark Zhandry}, booktitle = {CRYPTO~2023, Part~IV}, editor = {Helena Handschuh and Anna Lysyanskaya}, month = aug, pages = {263--293}, publisher = {Springer, Cham}, series = {{LNCS}}, title = {Computational Wiretap Coding from Indistinguishability Obfuscation}, volume = {14084}, year = {2023} } | |||||||||
Security-Preserving Distributed Samplers: How to Generate any CRS in One Round without Random Oracles
|

| ||||||||
|
A distributed sampler is a way for several mutually distrusting parties to
non-interactively generate a common reference string (CRS) that all parties trust.
Previous work constructs distributed samplers in the random oracle model, or in the
standard model with very limited security guarantees. This is no accident, as standard
model distributed samplers with full security were shown impossible.
In this work, we provide new definitions for distributed samplers which we show achieve meaningful security guarantees in the standard model. In particular, our notion implies that the hardness of a wide range of security games is preserved when the CRS is replaced with a distributed sampler. We also show how to realize our notion of distributed samplers. A core technical tool enabling our construction is a new notion of single-message zero knowledge.
@inproceedings{C:AbrWatZha23,
author = {Damiano Abram and Brent Waters and Mark Zhandry}, booktitle = {CRYPTO~2023, Part~I}, editor = {Helena Handschuh and Anna Lysyanskaya}, month = aug, pages = {489--514}, publisher = {Springer, Cham}, series = {{LNCS}}, title = {Security-Preserving Distributed Samplers: How to Generate Any {CRS} in One Round Without Random Oracles}, volume = {14081}, year = {2023} } | |||||||||
Tracing Quantum State Distinguishers via Backtracking
|

|

|

| ||||||
|
We show the following results:
• The post-quantum equivalence of indisitnguishability obfuscation and differing inputs obfuscation in the restricted setting where the outputs differ on at most a polynomial number of points. Our result handles the case where the auxiliary input may contain a quantum state; previous results could only handle classical auxiliary input. • Bounded collusion traitor tracing from general public key encryption, where the decoder is allowed to contain a quantum state. The parameters of the scheme grow polynomially in the collusion bound. • Collusion-resistant traitor tracing with constant-size ciphertexts from general public key encryption, again for quantum state decoders. The public key and secret keys grow polynomially in the number of users. • Traitor tracing with embedded identities in the keys, again for quantum state decoders, under a variety of different assumptions with different parameter size trade-offs. Traitor tracing and differing inputs obfuscation with quantum decoders / auxiliary input arises naturally when considering the post-quantum security of these primitives. We obtain our results by abstracting out a core algorithmic model, which we call the Back One Step (BOS) model. We prove a general theorem, reducing many quantum results including ours to designing \emph{classical} algorithms in the BOS model. We then provide simple algorithms for the particular instances studied in this work.
@inproceedings{C:Zhandry23,
author = {Mark Zhandry}, booktitle = {CRYPTO~2023, Part~V}, editor = {Helena Handschuh and Anna Lysyanskaya}, month = aug, pages = {3--36}, publisher = {Springer, Cham}, series = {{LNCS}}, title = {Tracing Quantum State Distinguishers via Backtracking}, volume = {14085}, year = {2023} } | |||||||||
Adaptive Multiparty NIKE
|

| ||||||||
|
We construct adaptively secure multiparty non-interactive key exchange (NIKE) from
polynomially-hard indistinguishability obfuscation and other standard assumptions.
This improves on all prior such protocols, which required sub-exponential hardness.
Along the way, we establish several compilers which simplify the task of constructing
new multiparty NIKE protocols, and also establish a close connection with a particular
type of constrained PRF.
@inproceedings{TCC:KopWatZha22,
author = {Venkata Koppula and Brent Waters and Mark Zhandry}, booktitle = {TCC~2022, Part~II}, editor = {Eike Kiltz and Vinod Vaikuntanathan}, month = nov, pages = {244--273}, publisher = {Springer, Heidelberg}, series = {{LNCS}}, title = {Adaptive Multiparty {NIKE}}, volume = {13748}, year = {2022} } | |||||||||
Collusion-Resistant Copy-Protection for Watermarkable Functionalities
|

| ||||||||
|
Copy-protection is the task of encoding a program into a quantum state to prevent
illegal duplications. A line of recent works studied copy-protection schemes under
"1 -> 2 attacks": the adversary receiving one program copy can not produce two valid
copies. However, under most circumstances, vendors need to sell more than one copy of
a program and still ensure that no duplicates can be generated. In this work, we
initiate the study of collusion-resistant copy-protection in the plain model. Our
results are twofold:
• For the first time, we show that all major watermarkable functionalities can be copy-protected (including unclonable decryption, digital signatures, and PRFs). Among these, copy-protection of digital signature schemes is not known before. The feasibility of copy-protecting all watermarkable functionalities is an open question raised by Aaronson et al. (CRYPTO' 21) • We make all the above schemes k bounded collusion-resistant for any polynomial k, giving the first bounded collusion-resistant copy-protection for various functionalities in the plain model.
@inproceedings{TCC:LLQZ22,
author = {Jiahui Liu and Qipeng Liu and Luowen Qian and Mark Zhandry}, booktitle = {TCC~2022, Part~I}, editor = {Eike Kiltz and Vinod Vaikuntanathan}, month = nov, pages = {294--323}, publisher = {Springer, Heidelberg}, series = {{LNCS}}, title = {Collusion Resistant Copy-Protection for Watermarkable Functionalities}, volume = {13747}, year = {2022} } | |||||||||
Affine Determinant Programs: A Framework for Obfuscation and Witness Encryption
|

| ||||||||
|
An affine determinant program ADP: {0,1}n → {0,1} is specified
by a tuple (A,B1,…,Bn) of square matrices over
Fq and a function Eval: Fq → {0,1}, and is evaluated on x
∈ {0,1}n by computing Eval(det(A + ∑ xiBi)).
In this work, we suggest ADPs as a new framework for building general-purpose obfuscation and witness encryption. We provide evidence to suggest that constructions following our ADP-based framework may one day yield secure, practically feasible obfuscation. As a proof-of-concept, we give a candidate ADP-based construction of indistinguishability obfuscation for all circuits along with a simple witness encryption candidate. We provide cryptanalysis demonstrating that our schemes resist several potential attacks, and leave further cryptanalysis to future work. Lastly, we explore practically feasible applications of our witness encryption candidate, such as public-key encryption with near-optimal key generation.
@inproceedings{ITCS:BIJMSZ20,
author = {James Bartusek and Yuval Ishai and Aayush Jain and Fermi Ma and Amit Sahai and Mark Zhandry}, booktitle = {ITCS 2020}, editor = {Thomas Vidick}, month = jan, pages = {82:1--82:39}, publisher = {{LIPIcs}}, title = {Affine Determinant Programs: {A} Framework for Obfuscation and Witness Encryption}, volume = {151}, year = {2020} } | |||||||||
The Distinction Between Fixed and Random Generators in Group-Based Assumptions
|

| ||||||||
|
There is surprisingly little consensus on the precise role of the generator g in
group-based assumptions such as DDH. Some works consider g to be a fixed part of the
group description, while others take it to be random. We study this subtle distinction
from a number of angles.
• In the generic group model, we demonstrate the plausibility of groups in which random-generator DDH (resp. CDH) is hard but fixed-generator DDH (resp. CDH) is easy. We observe that such groups have interesting cryptographic applications. • We find that seemingly tight generic lower bounds for the Discrete-Log and CDH problems with preprocessing (Corrigan-Gibbs and Kogan, Eurocrypt 2018) are not tight in the sub-constant success probability regime if the generator is random. We resolve this by proving tight lower bounds for the random generator variants; our results formalize the intuition that using a random generator will reduce the effectiveness of preprocessing attacks. • We observe that DDH-like assumptions in which exponents are drawn from low-entropy distributions are particularly sensitive to the fixed- vs. random-generator distinction. Most notably, we discover that the Strong Power DDH assumption of Komargodski and Yogev (Eurocrypt 2018) used for non-malleable point obfuscation is in fact false precisely because it requires a fixed generator. In response, we formulate an alternative fixed-generator assumption that suffices for a new construction of non-malleable point obfuscation, and we prove the assumption holds in the generic group model. We also give a generic group proof for the security of fixed-generator, low-entropy DDH (Canetti, Crypto 1997).
@inproceedings{C:BarMaZha19,
author = {James Bartusek and Fermi Ma and Mark Zhandry}, booktitle = {CRYPTO~2019, Part~II}, editor = {Alexandra Boldyreva and Daniele Micciancio}, month = aug, pages = {801--830}, publisher = {Springer, Heidelberg}, series = {{LNCS}}, title = {The Distinction Between Fixed and Random Generators in Group-Based Assumptions}, volume = {11693}, year = {2019} } | |||||||||
Quantum Lightning Never Strikes the Same State Twice
|

|

|

| ||||||
|
Public key quantum money can be seen as a version of the quantum no-cloning theorem
that holds even when the quantum states can be verified by the adversary. In this
work, investigate quantum lightning, a formalization of "collision-free quantum
money" defined by Lutomirski et al. [ICS'10], where no-cloning holds even when the
adversary herself generates the quantum state to be cloned. We then study quantum
money and quantum lightning, showing the following results:
• We demonstrate the usefulness of quantum lightning beyond quantum money by showing several potential applications, such as generating random strings with a proof of entropy, to completely decentralized cryptocurrency without a block-chain, where transactions is instant and local. • We give win-win results for quantum money/lightning, showing that either signatures/hash functions/commitment schemes meet very strong recently proposed notions of security, or they yield quantum money or lightning. Given the difficulty in constructing public key quantum money, this gives some indication that natural schemes do attain strong security guarantees. • We construct quantum lightning under the assumed multi-collision resistance of random degree-2 systems of polynomials. Our construction is inspired by our win-win result for hash functions, and yields the first plausible standard model instantiation of a non-collapsing collision resistant hash function. This improves on a result of Unruh [Eurocrypt'16] that requires a quantum oracle. •We show that instantiating the quantum money scheme of Aaronson and Christiano [STOC'12] with indistinguishability obfuscation that is secure against quantum computers yields a secure quantum money scheme. This construction can be seen as an instance of our win-win result for signatures, giving the first separation between two security notions for signatures from the literature. Thus, we provide the first constructions of public key quantum money from several cryptographic assumptions. Along the way, we develop several new techniques including a new precise variant of the no-cloning theorem.
@inproceedings{EC:Zhandry19b,
author = {Mark Zhandry}, booktitle = {EUROCRYPT~2019, Part~III}, editor = {Yuval Ishai and Vincent Rijmen}, month = may, pages = {408--438}, publisher = {Springer, Heidelberg}, series = {{LNCS}}, title = {Quantum Lightning Never Strikes the Same State Twice}, volume = {11478}, year = {2019} } | |||||||||
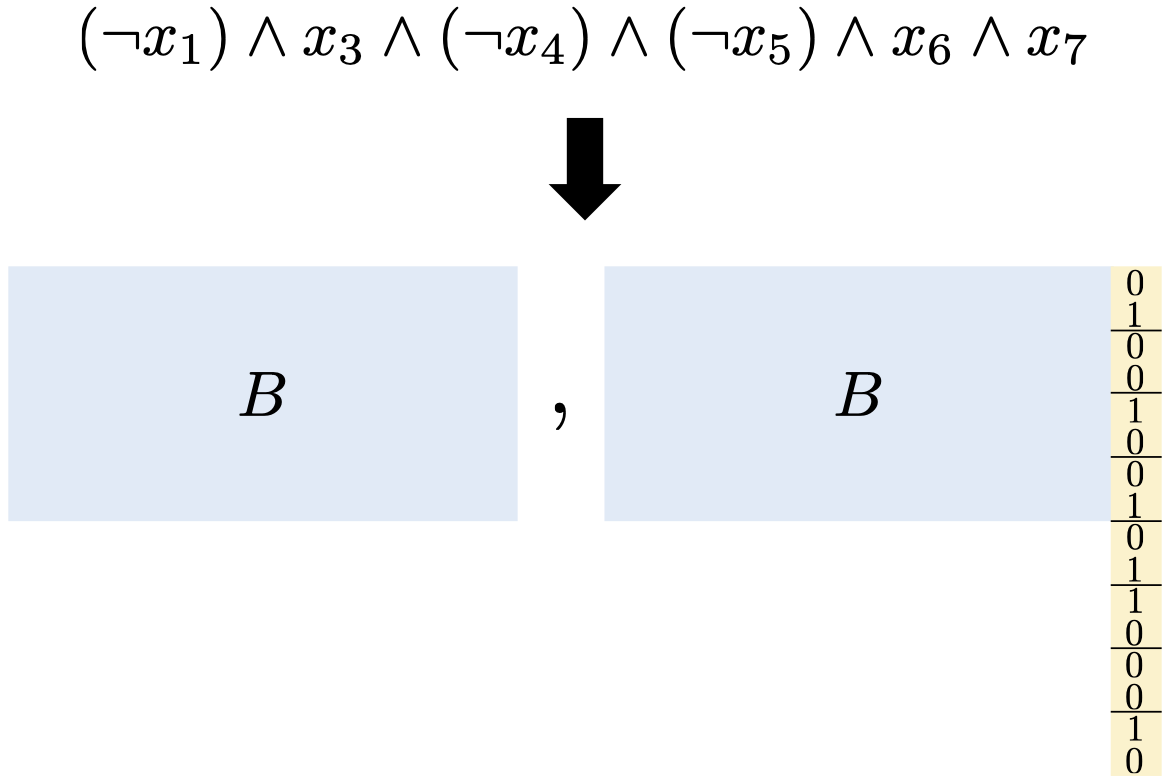
New Techniques for Obfuscating Conjunctions
|

| ||||||||
|
A conjunction is a function f(x1,...,xn) = ∧i ∈
S li where S ⊆ [n] and each li is xi or
¬ xi. Bishop et al. (CRYPTO 2018) recently proposed obfuscating
conjunctions by embedding them in the error positions of a noisy Reed-Solomon codeword
and placing the codeword in a group exponent. They prove distributional virtual black
box (VBB) security in the generic group model for random conjunctions where |S| ≥
0.226n. While conjunction obfuscation is known from LWE, these constructions rely on
substantial technical machinery.
In this work, we conduct an extensive study of simple conjunction obfuscation techniques. • We abstract the Bishop et al. scheme to obtain an equivalent yet more efficient "dual" scheme that handles conjunctions over exponential size alphabets. We give a significantly simpler proof of generic group security, which we combine with a novel combinatorial argument to obtain distributional VBB security for |S| of any size. • If we replace the Reed-Solomon code with a random binary linear code, we can prove security from standard LPN and avoid encoding in a group. This addresses an open problem posed by Bishop et al.~to prove security of this simple approach in the standard model. • We give a new construction that achieves information theoretic distributional VBB security and weak functionality preservation for |S| ≥ n - nδ and δ < 1. Assuming discrete log and δ < 1/2, we satisfy a stronger notion of functionality preservation for computationally bounded adversaries while still achieving information theoretic security.
@inproceedings{EC:BLMZ19,
author = {James Bartusek and Tancr{\'e}de Lepoint and Fermi Ma and Mark Zhandry}, booktitle = {EUROCRYPT~2019, Part~III}, editor = {Yuval Ishai and Vincent Rijmen}, month = may, pages = {636--666}, publisher = {Springer, Heidelberg}, series = {{LNCS}}, title = {New Techniques for Obfuscating Conjunctions}, volume = {11478}, year = {2019} } | |||||||||
The MMap Strikes Back: Obfuscation and New Multilinear Maps Immune to CLT13 Zeroizing Attacks
|

| ||||||||
|
We devise the first weak multilinear map model for CLT13 multilinear maps (Coron et
al., CRYPTO 2013) that captures all known classical polynomial-time attacks on the
maps. We then show important applications of our model. First, we show that in our
model, several existing obfuscation and order-revealing encryption schemes, when
instantiated with CLT13 maps, are secure against known attacks under a mild algebraic
complexity assumption used in prior work. These are schemes that are actually being
implemented for experimentation. However, until our work, they had no rigorous
justification for security.
Next, we turn to building constant degree multilinear maps on top of CLT13 for which there are no known attacks. Precisely, we prove that our scheme achieves the ideal security notion for multilinear maps in our weak CLT13 model, under a much stronger variant of the algebraic complexity assumption used above. Our multilinear maps do not achieve the full functionality of multilinear maps as envisioned by Boneh and Silverberg (Contemporary Mathematics, 2003), but do allow for re-randomization and for encoding arbitrary plaintext elements.
@inproceedings{TCC:MaZha18,
author = {Fermi Ma and Mark Zhandry}, booktitle = {TCC~2018, Part~II}, editor = {Amos Beimel and Stefan Dziembowski}, month = nov, pages = {513--543}, publisher = {Springer, Heidelberg}, series = {{LNCS}}, title = {The {MMap} Strikes Back: Obfuscation and New Multilinear Maps Immune to {CLT13} Zeroizing Attacks}, volume = {11240}, year = {2018} } | |||||||||
Preventing Zeroizing Attacks on GGH15
|

| ||||||||
|
The GGH15 multilinear maps have served as the foundation for a number of cutting-edge
cryptographic proposals. Unfortunately, many schemes built on GGH15 have been
explicitly broken by so-called "zeroizing attacks," which exploit leakage from honest
zero-test queries. The precise settings in which zeroizing attacks are possible have
remained unclear. Most notably, none of the current indistinguishability obfuscation
(iO) candidates from GGH15 have any formal security guarantees against zeroizing
attacks.
In this work, we demonstrate that all known zeroizing attacks on GGH15 implicitly construct algebraic relations between the results of zero-testing and the encoded plaintext elements. We then propose a "GGH15 zeroizing model" as a new general framework which greatly generalizes known attacks. Our second contribution is to describe a new GGH15 variant, which we formally analyze in our GGH15 zeroizing model. We then construct a new iO candidate using our multilinear map, which we prove secure in the GGH15 zeroizing model. This implies resistance to all known zeroizing strategies. The proof relies on the Branching Program Un-Annihilatability (BPUA) Assumption of Garg et al. [TCC 16-B] (which is implied by PRFs in NC^1 secure against P/Poly) and the complexity-theoretic p-Bounded Speedup Hypothesis of Miles et al. [ePrint 14] (a strengthening of the Exponential Time Hypothesis).
@inproceedings{TCC:BGMZ18,
author = {James Bartusek and Jiaxin Guan and Fermi Ma and Mark Zhandry}, booktitle = {TCC~2018, Part~II}, editor = {Amos Beimel and Stefan Dziembowski}, month = nov, pages = {544--574}, publisher = {Springer, Heidelberg}, series = {{LNCS}}, title = {Return of {GGH15}: Provable Security Against Zeroizing Attacks}, volume = {11240}, year = {2018} } | |||||||||
Decomposable Obfuscation: A Framework for Building Applications of Obfuscation From Polynomial Hardness
|

| ||||||||
|
There is some evidence that indistinguishability obfuscation (iO) requires either
exponentially many assumptions or (sub)exponentially hard assumptions, and indeed, all
known ways of building obfuscation suffer one of these two limitations. As such, any
application built from iO suffers from these limitations as well. However, for most
applications, such limitations do not appear to be inherent to the application, just
the approach using iO. Indeed, several recent works have shown how to base
applications of iO instead on functional encryption (FE), which can in turn be based
on the polynomial hardness of just a few assumptions. However, these constructions are
quite complicated and recycle a lot of similar techniques.
In this work, we unify the results of previous works in the form of a weakened notion of obfuscation, called Decomposable Obfuscation. We show (1) how to build decomposable obfuscation from functional encryption, and (2) how to build a variety of applications from decomposable obfuscation, including all of the applications already known from FE. The construction in (1) hides most of the difficult techniques in the prior work, whereas the constructions in (2) are much closer to the comparatively simple constructions from iO. As such, decomposable obfuscation represents a convenient new platform for obtaining more applications from polynomial hardness.
@inproceedings{TCC:LiuZha17,
author = {Qipeng Liu and Mark Zhandry}, booktitle = {TCC~2017, Part~I}, editor = {Yael Kalai and Leonid Reyzin}, month = nov, pages = {138--169}, publisher = {Springer, Heidelberg}, series = {{LNCS}}, title = {Decomposable Obfuscation: {A} Framework for Building Applications of Obfuscation from Polynomial Hardness}, volume = {10677}, year = {2017} } | |||||||||
Breaking the Sub-Exponential Barrier in Obfustopia
|

| ||||||||
|
Indistinguishability obfuscation (iO) has emerged as a surprisingly powerful notion.
Almost all known cryptographic primitives can be constructed from general purpose iO
and other minimalistic assumptions such as one-way functions. A major challenge in
this direction of research is to develop novel techniques for using iO since iO by
itself offers virtually no protection for secret information in the underlying
programs. When dealing with complex situations, often these techniques have to
consider an exponential number of hybrids (usually one per input) in the security
proof. This results in a sub-exponential loss in the security reduction.
Unfortunately, this scenario is becoming more and more common and appears to be a
fundamental barrier to many current techniques.
A parallel research challenge is building obfuscation from simpler assumptions. Unfortunately, it appears that such a construction would likely incur an exponential loss in the security reduction. Thus, achieving any application of iO from simpler assumptions would also require a sub-exponential loss, even if the iO-to-application security proof incurred a polynomial loss. Functional encryption (FE) is known to be equivalent to iO up to a sub-exponential loss in the FE-to-iO security reduction; yet, unlike iO, FE can be achieved from simpler assumptions (namely, specific multilinear map assumptions) with only a polynomial loss. In the interest of basing applications on weaker assumptions, we therefore argue for using FE as the starting point, rather than iO, and restricting to reductions with only a polynomial loss. By significantly expanding on ideas developed by Garg, Pandey, and Srinivasan (CRYPTO 2016), we achieve the following early results in this line of study: • We construct universal samplers based only on polynomially-secure public-key FE. As an application of this result, we construct a non-interactive multiparty key exchange (NIKE) protocol for an unbounded number of users without a trusted setup. Prior to this work, such constructions were only known from indistinguishability obfuscation. • We also construct trapdoor one-way permutations (OWP) based on polynomially-secure public-key FE. This improves upon the recent result of Bitansky, Paneth, and Wichs (TCC 2016) which requires iO of sub-exponential strength. We proceed in two steps, first giving a construction requiring iO of polynomial strength, and then specializing the FE-to-iO conversion to our specific application. Many of the techniques that have been developed for using iO, including many of those based on the "punctured programming" approach, become inapplicable when we insist on polynomial reductions to FE. As such, our results above require many new ideas that will likely be useful for future works on basing security on FE.
@inproceedings{EC:GPSZ17,
author = {Sanjam Garg and Omkant Pandey and Akshayaram Srinivasan and Mark Zhandry}, booktitle = {EUROCRYPT~2017, Part~III}, editor = {Jean-S{\'{e}}bastien Coron and Jesper Buus Nielsen}, month = apr # {~/~} # may, pages = {156--181}, publisher = {Springer, Heidelberg}, series = {{LNCS}}, title = {Breaking the Sub-Exponential Barrier in Obfustopia}, volume = {10212}, year = {2017} } | |||||||||
Encryptor Combiners: A Unified Approach to Multiparty NIKE, (H)IBE, and Broadcast Encryption
|

| ||||||||
|
We define the concept of an encryptor combiner. Roughly, such a combiner takes as
input n public keys for a public key encryption scheme, and produces a new combined
public key. Anyone knowing a secret key for one of the input public keys can learn the
secret key for the combined public key, but an outsider who just knows the input
public keys (who can therefore compute the combined public key for himself) cannot
decrypt ciphertexts from the combined public key. We actually think of public keys
more generally as encryption procedures, which can correspond to, say, encrypting to a
particular identity under an IBE scheme or encrypting to a set of attributes under an
ABE scheme.
We show that encryptor combiners satisfying certain natural properties can give natural constructions of multi-party non-interactive key exchange, low-overhead broadcast encryption, and hierarchical identity-based encryption. We then show how to construct two different encryptor combiners. Our first is built from universal samplers (which can in turn be built from indistinguishability obfuscation) and is sufficient for each application above, in some cases improving on existing obfuscation-based constructions. Our second is built from lattices, and is sufficient for hierarchical identity-based encryption. Thus, encryptor combiners serve as a new abstraction that (1) is a useful tool for designing cryptosystems, (2) unifies constructing hierarchical IBE from vastly different assumptions, and (3) provides a target for instantiating obfuscation applications from better tools.
@misc{EPRINT:MaZha17,
author = {Fermi Ma and Mark Zhandry}, howpublished = {Cryptology ePrint Archive, Report 2017/152}, note = {\url{https://eprint.iacr.org/2017/152}}, title = {Encryptor Combiners: {A} Unified Approach to Multiparty {NIKE}, ({H}){IBE}, and Broadcast Encryption}, year = {2017} } | |||||||||
How to Generate and use Universal Samplers
|

| ||||||||
|
The random oracle is an idealization that allows to model a hash function as an oracle
that will output a uniformly random string given an input. We introduce the notion of
universal sampler scheme as a method sampling securely from arbitrary
distributions.
We first motivate such a notion by describing several applications including generating the trusted parameters for many schemes from just a single trusted setup. We further demonstrate the versatility of universal sampler by showing how they give rise to applications such as identity-based encryption and multiparty key exchange. We give a solution in the random oracle model based on indistinguishability obfuscation. At the heart of our construction and proof is a new technique we call "delayed backdoor programming".
@inproceedings{AC:HJKSWZ16,
author = {Dennis Hofheinz and Tibor Jager and Dakshita Khurana and Amit Sahai and Brent Waters and Mark Zhandry}, booktitle = {ASIACRYPT~2016, Part~II}, editor = {Jung Hee Cheon and Tsuyoshi Takagi}, month = dec, pages = {715--744}, publisher = {Springer, Heidelberg}, series = {{LNCS}}, title = {How to Generate and Use Universal Samplers}, volume = {10032}, year = {2016} } | |||||||||
Secure Obfuscation in a Weak Multilinear Map Model
|

| ||||||||
|
All known candidate indistinguishibility obfuscation (iO) schemes rely on candidate
multilinear maps. Until recently, the strongest proofs of security available for iO
candidates were in a generic model that only allows "honest" use of the multilinear
map. Most notably, in this model the zero-test procedure only reveals whether an
encoded element is 0, and nothing more.
However, this model is inadequate: there have been several attacks on multilinear maps that exploit extra information revealed by the zero-test procedure. In particular, Miles, Sahai and Zhandry [Crypto'16] recently gave a polynomial-time attack on several iO candidates when instantiated with the multilinear maps of Garg, Gentry, and Halevi [Eurocrypt'13], and also proposed a new "weak multilinear map model" that captures all known polynomial-time attacks on GGH13. In this work, we give a new iO candidate which can be seen as a small modification or generalization of the original candidate of Garg, Gentry, Halevi, Raykova, Sahai, and Waters [FOCS'13]. We prove its security in the weak multilinear map model, thus giving the first iO candidate that is provably secure against all known polynomial-time attacks on GGH13. The proof of security relies on a new assumption about the hardness of computing annihilating polynomials, and we show that this assumption is implied by the existence of pseudorandom functions in NC1.
@inproceedings{TCC:GMMSSZ16,
author = {Sanjam Garg and Eric Miles and Pratyay Mukherjee and Amit Sahai and Akshayaram Srinivasan and Mark Zhandry}, booktitle = {TCC~2016-B, Part~II}, editor = {Martin Hirt and Adam D. Smith}, month = oct # {~/~} # nov, pages = {241--268}, publisher = {Springer, Heidelberg}, series = {{LNCS}}, title = {Secure Obfuscation in a Weak Multilinear Map Model}, volume = {9986}, year = {2016} } | |||||||||
The Magic of ELFs
|

|

|

| ||||||
|
We introduce the notion of an Extremely Lossy Function (ELF). An ELF is a
family of functions with an image size that is tunable anywhere from injective to
having a polynomial-sized image. Moreover, for any efficient adversary, for a
sufficiently large polynomial r (necessarily chosen to be larger than the running time
of the adversary), the adversary cannot distinguish the injective case from the case
of image size r.
We develop a handful of techniques for using ELFs, and show that such extreme lossiness is useful for instantiating random oracles in several settings. In particular, we show how to use ELFs to build secure point function obfuscation with auxiliary input, as well as polynomially-many hardcore bits for any one-way function. Such applications were previously known from strong knowledge assumptions — for example polynomially-many hardcore bits were only know from differing inputs obfuscation, a notion whose plausibility has been seriously challenged. We also use ELFs to build a simple hash function with output intractability, a new notion we define that may be useful for generating common reference strings. Next, we give a construction of ELFs relying on the exponential hardness of the decisional Diffie-Hellman problem, which is plausible in elliptic curve groups. Combining with the applications above, our work gives several practical constructions relying on qualitatively different — and arguably better — assumptions than prior works.
@inproceedings{C:Zhandry16,
author = {Mark Zhandry}, booktitle = {CRYPTO~2016, Part~I}, editor = {Matthew Robshaw and Jonathan Katz}, month = aug, pages = {479--508}, publisher = {Springer, Heidelberg}, series = {{LNCS}}, title = {The Magic of {ELFs}}, volume = {9814}, year = {2016} } | |||||||||
Annihilation Attacks for Multilinear Maps: Cryptanalysis of Indistinguishability Obfuscation over GGH13
|

| ||||||||
|
In this work, we put forward a new class of polynomial-time attacks on the original
multilinear maps of Garg, Gentry, and Halevi (2013). Previous polynomial-time attacks
on GGH13 were "zeroizing" attacks that generally required the availability of
low-level encodings of zero. Most significantly, such zeroizing attacks were not
applicable to candidate indistinguishability obfuscation (iO) schemes. iO has been the
subject of intense study.
To address this gap, we introduce annihilation attacks, which attack multilinear maps using non-linear polynomials. Annihilation attacks can work in situations where there are no low-level encodings of zero. Using annihilation attacks, we give the first polynomial-time cryptanalysis of candidate iO schemes over GGH13. More specifically, we exhibit two simple programs that are functionally equivalent, and show how to efficiently distinguish between the obfuscations of these two programs. Given the enormous applicability of iO, it is important to devise iO schemes that can avoid attack.
@inproceedings{C:MilSahZha16,
author = {Eric Miles and Amit Sahai and Mark Zhandry}, booktitle = {CRYPTO~2016, Part~II}, editor = {Matthew Robshaw and Jonathan Katz}, month = aug, pages = {629--658}, publisher = {Springer, Heidelberg}, series = {{LNCS}}, title = {Annihilation Attacks for Multilinear Maps: Cryptanalysis of Indistinguishability Obfuscation over {GGH13}}, volume = {9815}, year = {2016} } | |||||||||
Post-Zeroizing Obfuscation: New Mathematical Tools, and the Case of Evasive Circuits
|

|

| |||||||
|
Recent devastating attacks by Cheon et al.~[Eurocrypt'15] and others have highlighted
significant gaps in our intuition about security in candidate multilinear map schemes,
and in candidate obfuscators that use them. The new attacks, and some that were
previously known, are typically called "zeroizing" attacks because they all crucially
rely on the ability of the adversary to create encodings of 0.
In this work, we initiate the study of post-zeroizing obfuscation, and we present a construction for the special case of evasive functions. We show that our obfuscator survives all known attacks on the underlying multilinear maps, by proving that no encodings of 0 can be created by a generic-model adversary. Previous obfuscators (for both evasive and general functions) were either analyzed in a less-conservative "pre-zeroizing" model that does not capture recent attacks, or were proved secure relative to assumptions that are now known to be false. To prove security, we introduce a new technique for analyzing polynomials over multilinear map encodings. This technique shows that the types of encodings an adversary can create are much more restricted than was previously known, and is a crucial step toward achieving post-zeroizing security. We also believe the technique is of independent interest, as it yields efficiency improvements for existing schemes.
@inproceedings{EC:BMSZ16,
author = {Saikrishna Badrinarayanan and Eric Miles and Amit Sahai and Mark Zhandry}, booktitle = {EUROCRYPT~2016, Part~II}, editor = {Marc Fischlin and Jean-S{\'{e}}bastien Coron}, month = may, pages = {764--791}, publisher = {Springer, Heidelberg}, series = {{LNCS}}, title = {Post-zeroizing Obfuscation: New Mathematical Tools, and the Case of Evasive Circuits}, volume = {9666}, year = {2016} } | |||||||||
Anonymous Traitor Tracing: How to Embed Arbitrary Information in a Key
|

| ||||||||
|
In a traitor tracing scheme, each user is given a different decryption key. A content
distributor can encrypt digital content using a public encryption key and each user in
the system can decrypt it using her decryption key. Even if a coalition of users
combines their decryption keys and constructs some "pirate decoder" that is capable of
decrypting the content, there is a public tracing algorithm that is guaranteed to
recover the identity of at least one of the users in the coalition given black-box
access to such decoder.
In prior solutions, the users are indexed by numbers 1,…,N and the tracing algorithm recovers the index i of a user in a coalition. Such solutions implicitly require the content distributor to keep a record that associates each index i with the actual identifying information for the corresponding user (e.g., name, address, etc.) in order to ensure accountability. In this work, we construct traitor tracing schemes where all of the identifying information about the user can be embedded directly into the user's key and recovered by the tracing algorithm. In particular, the content distributor does not need to separately store any records about the users of the system, and honest users can even remain anonymous to the content distributor. The main technical difficulty comes in designing tracing algorithms that can handle an exponentially large universe of possible identities, rather than just a polynomial set of indices i∈[N]. We solve this by abstracting out an interesting algorithmic problem that has surprising connections with seemingly unrelated areas in cryptography. We also extend our solution to a full "broadcast-trace-and-revoke" scheme in which the traced users can subsequently be revoked from the system. Depending on parameters, some of our schemes can be based only on the existence of public-key encryption while others rely on indistinguishability obfuscation.
@inproceedings{EC:NisWicZha16,
author = {Ryo Nishimaki and Daniel Wichs and Mark Zhandry}, booktitle = {EUROCRYPT~2016, Part~II}, editor = {Marc Fischlin and Jean-S{\'{e}}bastien Coron}, month = may, pages = {388--419}, publisher = {Springer, Heidelberg}, series = {{LNCS}}, title = {Anonymous Traitor Tracing: How to Embed Arbitrary Information in a Key}, volume = {9666}, year = {2016} } | |||||||||
Order-Revealing Encryption and the Hardness of Private Learning
|

| ||||||||
|
An order-revealing encryption scheme gives a public procedure by which two ciphertexts
can be compared to reveal the ordering of their underlying plaintexts. We show how to
use order-revealing encryption to separate computationally efficient PAC learning from
efficient (ε,δ)-differentially private PAC learning. That is, we
construct a concept class that is efficiently PAC learnable, but for which every
efficient learner fails to be differentially private. This answers a question of
Kasiviswanathan et al. (FOCS '08, SIAM J. Comput. '11).
To prove our result, we give a generic transformation from an order-revealing encryption scheme into one with strongly correct comparison, which enables the consistent comparison of ciphertexts that are not obtained as the valid encryption of any message. We believe this construction may be of independent interest.
@inproceedings{TCC:BunZha16,
author = {Mark Bun and Mark Zhandry}, booktitle = {TCC~2016-A, Part~I}, editor = {Eyal Kushilevitz and Tal Malkin}, month = jan, pages = {176--206}, publisher = {Springer, Heidelberg}, series = {{LNCS}}, title = {Order-Revealing Encryption and the Hardness of Private Learning}, volume = {9562}, year = {2016} } | |||||||||
Cutting-Edge Cryptography Through the Lens of Secret Sharing
|

| ||||||||
|
Secret sharing is a mechanism by which a trusted dealer holding a secret "splits" a
secret into many "shares" and distributes the shares to a collection of parties.
Associated with the sharing is a monotone access structure, that specifies which
parties are "qualified" and which are not: any qualified subset of parties can
(efficiently) reconstruct the secret, but no unqualified subset can learn anything
about the secret. In the most general form of secret sharing, the access structure
can be any monotone NP language.
In this work, we consider two very natural extensions of secret sharing. In the first, which we call distributed secret sharing, there is no trusted dealer at all, and instead the role of the dealer is distributed amongst the parties themselves. Distributed secret sharing can be thought of as combining the features of multiparty non-interactive key exchange and standard secret sharing, and may be useful in settings where the secret is so sensitive that no one individual dealer can be trusted with the secret. Our second notion is called functional secret sharing, which incorporates some of the features of functional encryption into secret sharing by providing more fine-grained access to the secret. Qualified subsets of parties do not learn the secret, but instead learn some function applied to the secret, with each set of parties potentially learning a different function. Our main result is that both of the extensions above are equivalent to several recent cutting-edge primitives. In particular, general-purpose distributed secret sharing is equivalent to witness PRFs, and general-purpose functional secret sharing is equivalent to indistinguishability obfuscation. Thus, our work shows that it is possible to view some of the recent developments in cryptography through a secret sharing lens, yielding new insights about both these cutting-edge primitives and secret sharing.
@inproceedings{TCC:KomZha16,
author = {Ilan Komargodski and Mark Zhandry}, booktitle = {TCC~2016-A, Part~II}, editor = {Eyal Kushilevitz and Tal Malkin}, month = jan, pages = {449--479}, publisher = {Springer, Heidelberg}, series = {{LNCS}}, title = {Cutting-Edge Cryptography Through the Lens of Secret Sharing}, volume = {9563}, year = {2016} } | |||||||||
Adaptively Secure Broadcast Encryption with Small System Parameters
|

| ||||||||
|
We build the first public-key broadcast encryption systems that simultaneously achieve
adaptive security against arbitrary number of colluders, have small system parameters,
and have security proofs that do not rely on knowledge assumptions or complexity
leveraging. Our schemes are built from either composite order multilinear maps or
obfuscation and enjoy a ciphertext overhead, private key size, and public key size
that are all poly-logarithmic in the total number of users. Previous broadcast
schemes with similar parameters are either proven secure in a weaker static model, or
rely on non-falsifiable knowledge assumptions.
@misc{EPRINT:Zhandry14b,
author = {Mark Zhandry}, howpublished = {Cryptology ePrint Archive, Report 2014/757}, note = {\url{https://eprint.iacr.org/2014/757}}, title = {Adaptively Secure Broadcast Encryption with Small System Parameters}, year = {2014} } | |||||||||
Multiparty Key Exchange, Efficient Traitor Tracing, and More from Indistinguishability Obfuscation
|

|

| |||||||
|
In this work, we show how to use indistinguishability obfuscation (iO) to build
multiparty key exchange, efficient broadcast encryption, and efficient traitor
tracing. Our schemes enjoy several interesting properties that have not been
achievable before:
• Our multiparty non-interactive key exchange protocol does not require a trusted setup. Moreover, the size of the published value from each user is independent of the total number of users. • Our broadcast encryption schemes support distributed setup, where users choose their own secret keys rather than be given secret keys by a trusted entity. The broadcast ciphertext size is independent of the number of users. • Our traitor tracing system is fully collusion resistant with short ciphertexts, secret keys, and public key. Ciphertext size is logarithmic in the number of users and secret key size is independent of the number of users. Our public key size is polylogarithmic in the number of users. The recent functional encryption system of Garg, Gentry, Halevi, Raykova, Sahai, and Waters also leads to a traitor tracing scheme with similar ciphertext and secret key size, but the construction in this paper is simpler and more direct. These constructions resolve an open problem relating to differential privacy. • Generalizing our traitor tracing system gives a private broadcast encryption scheme (where broadcast ciphertexts reveal minimal information about the recipient set) with optimal size ciphertext. Several of our proofs of security introduce new tools for proving security using indistinguishability obfuscation.
@inproceedings{C:BonZha14,
author = {Dan Boneh and Mark Zhandry}, booktitle = {CRYPTO~2014, Part~I}, editor = {Juan A. Garay and Rosario Gennaro}, month = aug, pages = {480--499}, publisher = {Springer, Heidelberg}, series = {{LNCS}}, title = {Multiparty Key Exchange, Efficient Traitor Tracing, and More from Indistinguishability Obfuscation}, volume = {8616}, year = {2014} } | |||||||||
Differing-Inputs Obfuscation and Applications
|

| ||||||||
|
In this paper, we study of the notion of differing-input obfuscation, introduced by
Barak et al. (CRYPTO 2001,JACM 2012). For any two circuits
C0 and
C1, a differing-input obfuscator diO guarantees that the
non-existence of a adversary that can find an input on which C0 and
C1 differ implies that diO(C0) and diO(C1) are
computationally indistinguishable. We show many applications of this notion:• We define the notion of a differing-input obfuscator for Turing machines and give a construction for the same (without converting it to a circuit) with input-specific running times. More specifically, for each input, our obfuscated Turning machine takes time proportional to the running time of the Turing machine on that specific input rather than the machine\'s worst-case running time. • We give a functional encryption scheme that is fully-secure even when the adversary can obtain an unbounded number of secret keys. Furthermore, our scheme allows for secret-keys to be associated with Turing machines and thereby achieves input-specific running times and can be equipped with delegation properties. We stress that this is the first functional encryption scheme with security for an unbounded number of secret keys satisfying any of these properties. • We construct a multi-party non-interactive key exchange protocol with no trusted setup where all parties post only logarithmic-size messages. It is the first such scheme with such short messages. We similarly obtain a broadcast encryption system where the ciphertext overhead and secret-key size is constant (i.e. independent of the number of users), and the public key is logarithmic in the number of users. Both our constructions make inherent use of the power provided by differing-input obfuscation. It is not currently known how to construct systems with these properties from the weaker notion of indistinguishability obfuscation.
@misc{EPRINT:ABGSZ13,
author = {Prabhanjan Ananth and Dan Boneh and Sanjam Garg and Amit Sahai and Mark Zhandry}, howpublished = {Cryptology ePrint Archive, Report 2013/689}, note = {\url{https://eprint.iacr.org/2013/689}}, title = {Differing-Inputs Obfuscation and Applications}, year = {2013} } | |||||||||