Consider a state-level adversary who observes and stores large amounts of encrypted data from all users on the Internet, but does not have the capacity to store it all. Later, it may target certain "persons of interest" in order to obtain their decryption keys. We would like to guarantee that, if the adversary`s storage capacity is only (say) 1% of the total encrypted data size, then even if it can later obtain the decryption keys of arbitrary users, it can only learn something about the contents of (roughly) 1%$ of the ciphertexts, while the rest will maintain full security. This can be seen as an extension of incompressible cryptography (Dziembowski CRYPTO '06, Guan, Wichs and Zhandry EUROCRYPT '22) to the multi-user setting. We provide solutions in both the symmetric key and public key setting with various trade-offs in terms of computational assumptions and efficiency.

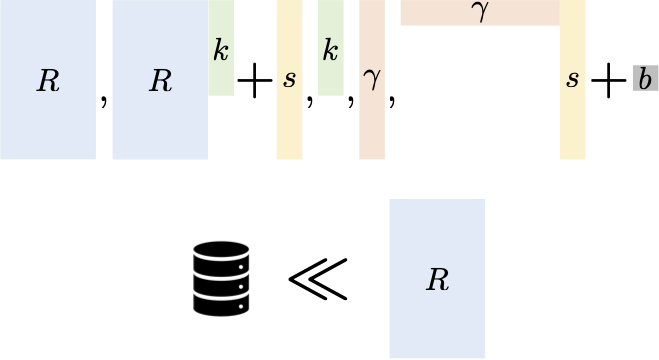
As the core technical tool, we study an information-theoretic problem which we refer to as "milt-instance randomness extraction." Suppose X₁, ..., X_t are correlated random variables whose total joint min-entropy rate is α, but we know nothing else about their individual entropies. We choose $t$ random and independent seeds S₁,...,S_t and attempt to individually extract some small amount of randomness Y_i = Ext(X_i;S_i) from each X_i. We'd like to say that roughly an α-fraction of the extracted outputs Y_i should be indistinguishable from uniform even given all the remaining extracted outputs and all the seeds. We show that this indeed holds for specific extractors based on Hadamard and Reed-Muller codes.

@inproceedings{TCC:GuaWicZha23,
    author =        {Jiaxin Guan and Daniel Wichs and Mark Zhandry},
    booktitle =     {TCC~2023, Part~III},
    editor =        {Guy N. Rothblum and Hoeteck Wee},
    month =         nov # {~/~} # dec,
    pages =         {93--122},
    publisher =     {Springer, Cham},
    series =        {{LNCS}},
    title =         {Multi-instance Randomness Extraction and Security
                     Against Bounded-Storage Mass Surveillance},
    volume =        {14371},
    year =          {2023}
}

Incompressible encryption allows us to make the ciphertext size flexibly large and ensures that an adversary learns nothing about the encrypted data, even if the decryption key later leaks, unless she stores essentially the entire ciphertext. Incompressible signatures can be made arbitrarily large and ensure that an adversary cannot produce a signature on any message, even one she has seen signed before, unless she stores one of the signatures essentially in its entirety.

In this work, we give simple constructions of both incompressible public-key encryption and signatures under minimal assumptions. Furthermore, large incompressible ciphertexts (resp. signatures) can be decrypted (resp. verified) in a streaming manner with low storage. In particular, these notions strengthen the related concepts of disappearing encryption and signatures, recently introduced by Guan and Zhandry (TCC 2021), whose previous constructions relied on sophisticated techniques and strong, non-standard assumptions. We extend our constructions to achieve an optimal "rate", meaning the large ciphertexts (resp. signatures) can contain almost equally large messages, at the cost of stronger assumptions.

@inproceedings{EC:GuaWicZha22,
  author =        {Jiaxin Guan and Daniel Wichs and Mark Zhandry},
  booktitle =     {EUROCRYPT~2022, Part~I},
  editor =        {Orr Dunkelman and Stefan Dziembowski},
  month =         may # {~/~} # jun,
  pages =         {700--730},
  publisher =     {Springer, Heidelberg},
  series =        {{LNCS}},
  title =         {Incompressible Cryptography},
  volume =        {13275},
  year =          {2022},
}

In this work, we study disappearing cryptography in the bounded storage model. Here, a component of the transmission, say a ciphertext, a digital signature, or even a program, is streamed bit by bit. The stream is so large for anyone to store in its entirety, meaning the transmission effectively disappears once the stream stops.

We first propose the notion of online obfuscation, capturing the goal of disappearing programs in the bounded storage model. We give a negative result for VBB security in this model, but propose candidate constructions for a weaker security goal, namely VGB security. We then demonstrate the utility of VGB online obfuscation, showing that it can be used to generate disappearing ciphertexts and signatures. All of our applications are not possible in the standard model of cryptography, regardless of computational assumptions used.

@inproceedings{TCC:GuaZha21,
    author =        {Jiaxin Guan and Mark Zhandry},
    booktitle =     {TCC~2021, Part~II},
    editor =        {Kobbi Nissim and Brent Waters},
    title =         {Disappearing Cryptography in the Bounded Storage Model},
    month =         nov,
    pages =         {365--396},
    publisher =     {Springer, Heidelberg},
    series =        {{LNCS}},
    volume =        {13043},
    title =         {Disappearing Cryptography in the Bounded Storage Model},
    year =          {2021}
}

The bounded storage model promises unconditional security proofs against computationally unbounded adversaries, so long as the adversary's space is bounded. In this work, we develop simple new constructions of two-party key agreement, bit commitment, and oblivious transfer in this model. In addition to simplicity, our constructions have several advantages over prior work, including an improved number of rounds and enhanced correctness. Our schemes are based on Raz's lower bound for learning parities.

@inproceedings{EC:GuaZha19,
    author =        {Jiaxin Guan and Mark Zhandary},
    booktitle =     {EUROCRYPT~2019, Part~III},
    editor =        {Yuval Ishai and Vincent Rijmen},
    month =         may,
    pages =         {500--524},
    publisher =     {Springer, Heidelberg},
    series =        {{LNCS}},
    title =         {Simple Schemes in the Bounded Storage Model},
    volume =        {11478},
    year =          {2019}
}